​质数和合数,质数和合数是什么

质数和合数,质数和合数是什么

本文目录

1.质数和合数是什么 2.质数和合数的定义 3.什么是质数和合数 4.20以内的质数和合数各有哪些

质数和合数是什么

质数（prime number）又称素数，有无限个。质数定义为在大于1的自然数中，除了1和它本身以外不再有其他因数。

合数指自然数中除了能被1和本身整除外，还能被其他数（0除外）整除的数。与之相对的是质数，而1既不属于质数也不属于合数。最小的合数是4。其中，完全数与相亲数是以它为基础的。

扩展资料：

一、质数的数目计算

1、在一个大于1的数a和它的2倍之间（即区间（a, 2a]中）必存在至少一个素数。

2、存在任意长度的素数等差数列。

3、一个偶数可以写成两个合数之和，其中每一个合数都最多只有9个质因数。（挪威数学家布朗，1920年）

4、一个偶数必定可以写成一个质数加上一个合成数，其中合数的因子个数有上界。（瑞尼，1948年）

二、合数的相关性质

1、所有大于2的偶数都是合数。

2、所有大于5的奇数中，个位为5的都是合数。

3、除0以外，所有个位为0的自然数都是合数。

4、所有个位为4，6，8的自然数都是合数。

5、最小的（偶）合数为4，最小的奇合数为9。

三、相关概念

只有1和它本身两个因数的自然数，叫质数（或称素数）。（如：由2÷1=2，2÷2=1，可知2的因数只有1和它本身2这两个因数，所以2就是质数。

与之相对立的是合数：“除了1和它本身两个因数外，还有其它因数的数，叫合数。”如：4÷1=4，4÷2=2，4÷4=1，很显然，4的因数除了1和它本身4这两个因数以外，还有因数2，所以4是合数。）

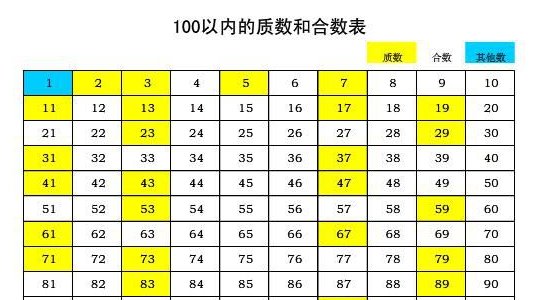
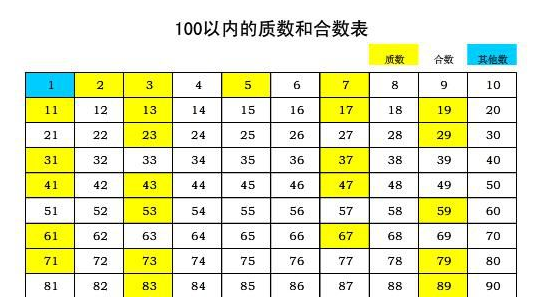
100以内的质数有2、3、5、7、11、13、17、19、23、29、31、37、41、43、47、53、59、61、67、71、73、79、83、89、97，一共有25个。

参考资料来源：百度百科-质数

参考资料来源：百度百科-合数

质数和合数的定义

质数（prime number）又称素数，有无限个。质数定义为在大于1的自然数中，除了1和它本身以外不再有其他因数。

合数指自然数中除了能被1和本身整除外，还能被其他数（0除外）整除的数。与之相对的是质数，而1既不属于质数也不属于合数。最小的合数是4。其中，完全数与相亲数是以它为基础的。

扩展资料：

一、质数性质

1、质数p的约数只有两个：1和p。

2、初等数学基本定理：任一大于1的自然数，要么本身是质数，要么可以分解为几个质数之积，且这种分解是唯一的。

3、质数的个数是无限的。

4、质数的个数公式π（n）是不减函数。

5、若n为正整数，在n²到（n+1）²之间至少有一个质数。

二、合数性质

1、所有大于2的偶数都是合数。

2、所有大于5的奇数中，个位为5的都是合数。

3、除0以外，所有个位为0的自然数都是合数。

4、所有个位为4，6，8的自然数都是合数。

5、最小的（偶）合数为4，最小的奇合数为9。

6、每一个合数都可以以唯一形式被写成质数的乘积，即分解质因数。

参考资料来源：百度百科-质数

参考资料来源：百度百科-合数

什么是质数和合数

质数又称素数。是一个大于1的自然数，并且因数只有1和它自身，不能整除其他自然数。合数则因数除了1和本身还有其他因数的数。

扩展资料：

质数的性质：

质数的个数是无穷的。欧几里得的《几何原本》中有一个经典的证明。它使用了证明常用的方法：反证法。具体证明如下：假设质数只有有限的n个，从小到大依次排列为p1，p2，……，pn，设N=p1×p2×……×pn，那么，N+1是素数或者不是素数。

如果N+1为素数，则N+1要大于p1，p2，……，pn，所以它不在那些假设的素数集合中。

1、如果 为合数，因为任何一个合数都可以分解为几个素数的积；而N和N+1的最大公约数是1，所以不可能被p1，p2，……，pn整除，所以该合数分解得到的素因数肯定不在假设的素数集合中。因此无论该数是素数还是合数，都意味着在假设的有限个素数之外还存在着其他素数。所以原先的假设不成立。也就是说，素数有无穷多个。

2、其他数学家给出了一些不同的证明。欧拉利用黎曼函数证明了全部素数的倒数之和是发散的，恩斯特·库默的证明更为简洁，哈里·弗斯滕伯格则用拓扑学加以证明。

参考资料：质数-百度百科

20以内的质数和合数各有哪些

质数：大于1的自然数，除了一和它本身之外，不能被其他数整除的正整数，是质数，又称素数。

合数是除了质数以外的数（大于1的自然数），即除了一和它本身以外，还有其他的因数的正整数。

1既不是质数，又不是合数。

例如：2、3、5、7是质数。4、6、8、9、10是合数。

拓展资料：

两个或两个以上素数的乘积，可以组成一个合数，并且只可以组成一个合数。反之，一个合数可以拆分为一组素数的乘积，并且只可以拆分为一组素数的乘积。

以上就是关于质数和合数,质数和合数是什么的全部内容，以及zhishu的相关内容,希望能够帮到您。