​割线是什么

割线是什么

割线是什么

2021年浙江杭州的这道中考关于圆的综合问题，还是蛮有个性的。第一小题很有创意，题型不算新，但在圆中看到这样的列表法求函数解析式的情形，还是比较少见的。只要能适应，就是送分题。第二小题就比较烧脑。如果借用老教材的“割线定理”，就会比较容易解决。

如图，△ABC内接于⊙O，点C在劣弧AB上(不与点A,B重合)，点D为弦BC的中点，DE⊥BC，DE与AC的延长线交于点E，射线AO与射线EB交于点F，与⊙O交于点G，设∠GAB=α，∠ACB=β，∠EAG+∠EBA=γ.

(1)点点同学通过画图和测量得到以下近似数据：

α

30度

40度

50度

60度

β

120度

130度

140度

150度

γ

150度

140度

130度

120度

猜测： β关于α的函数表达式， γ关于α的函数表达式，并给出证明；

(2)假设γ=135⁰，CD=3，△ABE的面积为△ABC的面积的4倍，求⊙O半径的长.

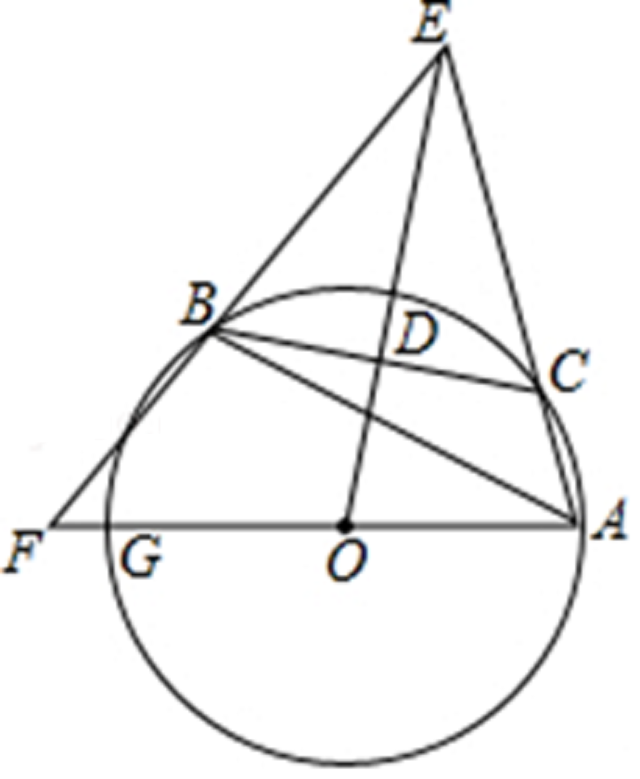
解：(1)猜想： β=α+90度, γ=180度-α. 理由如下：【说是猜想，其实已经在草稿纸上画出来了，八九不离十】

连接CG, 则∠ACG=90度, ∠BCG=∠GAB,【由于作辅助线之后，两个图形过于相似，所以这里先不提供，以防系统误判图形重复】

∠ACB=∠ACG+∠BCG=90度+∠GAB, 即β=α+90度；

∵DE⊥BC, CG⊥AE, ∴∠BCG=∠CED=α,【这是“两边互相垂直的两个锐角相等”定理的应用。也可以由“直角三角形斜边上的高将直角三角形分成与原三角形相似的两个直角三角形”推出这对角相等的关系，后者会比较麻烦，使得解题过程非常繁琐，前者就很简便，但前面这个定理，会用的考生可能不多。学了老黄的解题过程，以后就会用了】

又点D为弦BC的中点，∴∠BEC=2∠CED=2α,【这是等腰三角形底边“三线合一”的灵活应用】

γ=∠EAG+∠EBA=∠GAB+∠BAE+∠EBA=∠BAE+∠EBA+α

=∠BAE+∠EBA+2α-α=∠BAE+∠EBA+∠BEC-α=180⁰-α.

(2)当γ=135⁰时, α=180⁰-β=45⁰，∠BEC=2α=90⁰,【可以看到原图非常不准确。图形不准确往往对解题有比较大的影响。但是这里想画准确的图形，很困难，而且画出来的图看着会叫人难受，如下图。像这样的图，在考场上画出来，很不划算。】

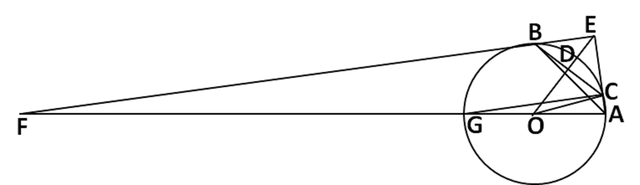
△BCE是等腰直角三角形, BE=CE=根号2CD=3根号2,

∵S△ABE=4S△ABC, ∴AE=4AC，∴AC=CE/3=根号2，【接下来运用割线定理，就可以轻松很多，由于割线定理没有出现在当前的教材里，所以要注明一下，就可以了。】

记OE交⊙O于点H，HE=x，则x(x+2r)=CE(CE+AC)=24(割线定理),【如果不用割线定理，就相当于要证明一次割线定理。割线定理：从圆外一点引圆的两条割线，这一点到每条割线与圆交点的距离的积相等】

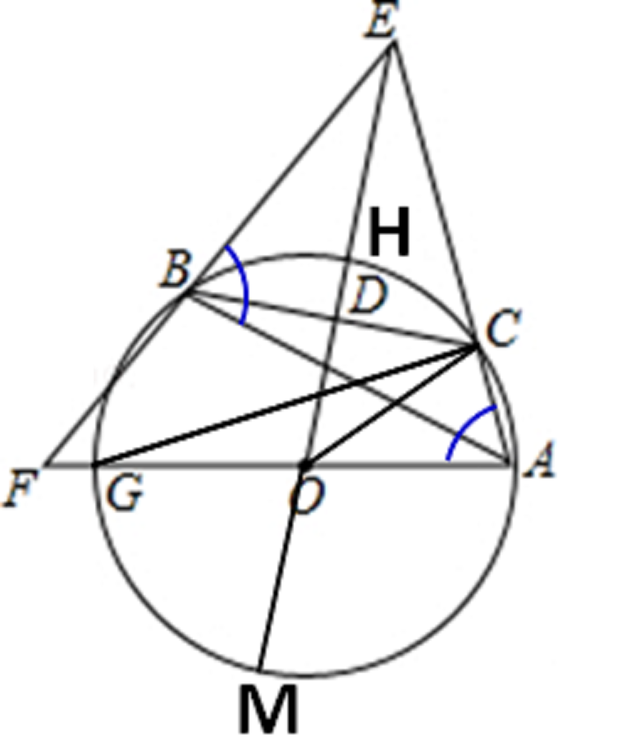
即x^2+2rx=24,

连接OC，

在Rt△OCD中，CD^2=OD^2+CD^2=(OF+EF-ED)^2+CD^2=(OF+EF-CD)^2+CD^2，

即r^2=(r+x-3)^2+9=r^2+x^2+9+2rx-6r-6x+9,【事实上，这里已经得到了一个关于x,r的二元方程组，可以直接解出r的值了】

∴x^2+2rx-6r-6x+18=42-6r-6x=0, r+x=7, r^2=42+9=25,

解得r=5或r=-5(舍去), ∴⊙O半径的长为5.

怎么样？割线定理是不是很好用啊？